Source Transformation Problems with Solutions

by
figure 1 source transformation

Source transformation is a circuit analysis technique in which we convert voltage source in series with resistor into a current source in parallel with the resistor and vice versa.

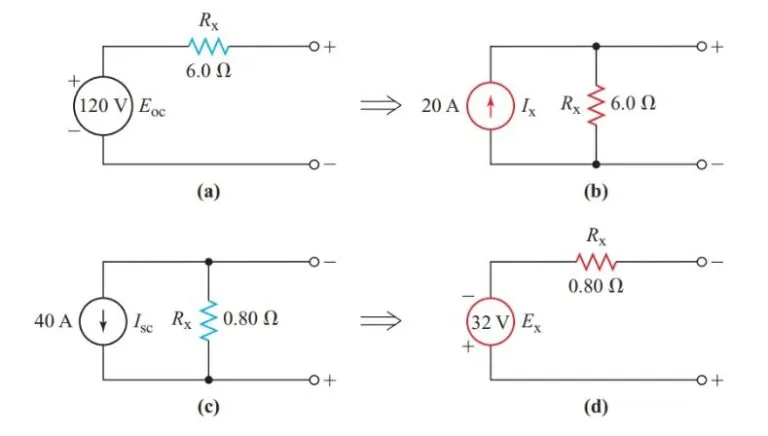
Figure 1 depicts an example of an equivalent constant-current source for a given constant-voltage source, where Rint is the same value but appears in parallel with the ideal current source.

The Rint in the constant-voltage source is the same value as in the constant-current source, but it is connected in series with the ideal voltage source.

A resistance Rx connected in series with an ideal voltage source allows us to convert the source from a voltage to a current.

A voltage source (Vs) in series with a resistor (Rx) can be the source’s internal resistance or an external network resistor.

Similarly, a constant-voltage source cannot replace an ideal current source without some form of resistance in parallel with the former.

The short-circuit current, Ix, for the equivalent constant-current source, shown in Figure 1(b), is calculated by plugging the values of V and I into Equation 1.

figure 0.1

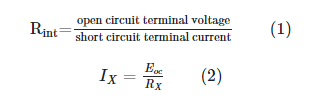
Similarly, given the constant-current source of Figure 1(c), Ex for the equivalent constant-voltage source of Figure 1(d) is the open-circuit voltage:

EX = IscRX (3)

figure 1 source transformation
figure 1 source transformation

Source Transformation Example

  • A voltage source with an open-circuit voltage of 120 V and an internal resistance of 6.0 V has to be converted into an equivalent constant-current source.
  • Using a current source that outputs 40 A at a constant voltage of 0.80 V, find the constant-voltage source that is equivalent.
  • Verify that when a 12-V load is applied to the equivalent sources in (a), the same results are obtained.

Solution

  • Both the constant-current source and the voltage source have the same internal resistance, Rint 5 6.0 V.
figure 1.1
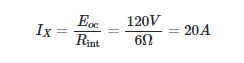
  • The constant-voltage equivalent source has the same Rint as the constant-current source.
figure 1.2
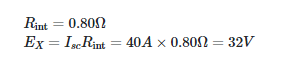
  • By connecting a 12-volt load to the power supply shown in Figure 1(a)
figure 1.3

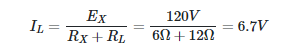
and,

figure 1.4
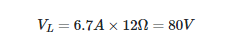
  • By connecting a 12-volt load to the power supply shown in Figure 1(b)
figure 1.5

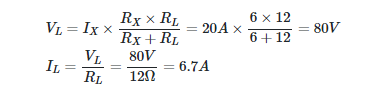
Once we understand the concept, we can easily do the mental math required to convert voltage sources into equivalent current sources (and vice versa) when conducting network analysis. Resistor networks with voltage and current sources are common in transistor circuit analysis. Solving such networks is typically simplified by converting the sources to either voltage or current.

Related Articles: