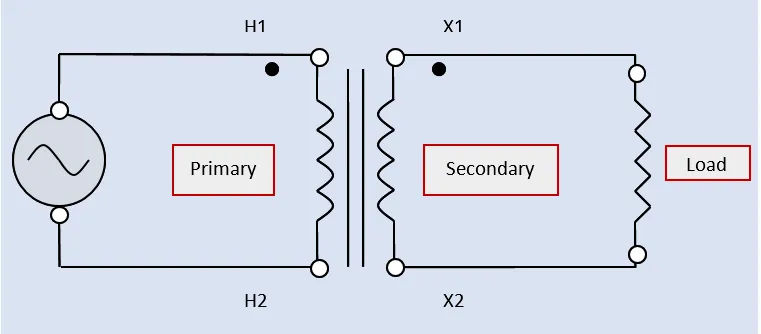
There are three primary transformer ratios in any single-phase AC transformer: the current ratio, the turns ratio, and the voltage ratio. The turns ratio, determined during production, affects both the current and voltage ratios (by the number of wraps of wire in each respective winding).
The voltage rating of a transformer is determined by the number of turns or wraps of wire around the iron core. Wire that is coiled or coiled around another object serves as an inductive reactor in the primary or secondary circuit. Coils (windings) are typically measured in terms of inductive reactance, but in this context, they are measured in terms of voltage.
The number of turns or wraps of wire in each of the circuits in Figure 1 establishes the maximum allowable voltage for that circuit.
The number of turns in a transformer’s winding increases when either the primary or secondary circuit has a high voltage rating. The number of turns in a transformer’s winding will be small if either the primary or secondary circuit has a low voltage rating. When comparing voltage to turns, you’ll find a direct correlation. In a nutshell:
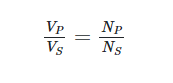
Where
V ( ) = the voltage rating in the primary (P) and secondary (S) circuits
N ( ) = the number of turns in the primary (P) and secondary (S) circuits
The ratio of the primary voltage to the secondary voltage, which is directly proportional to the turns ratio of the transformer, is expressed as a fraction of a power of 1.
As an illustration, the turns ratio of a step-down transformer with a voltage ratio of 30:1 would be written as 30:1. (30:1).
Stepping up the supply voltage with a transformer involves expressing the ratio of the primary voltage to the secondary voltage as a value between 1 and some multiple of 1. This ratio, called the turns ratio, determines how much of a boost the transformer provides.
If the voltage ratio of a step-up transformer is 55 to 1, then the turns ratio would be written as 1 to 55. (1:55).
A transformer’s primary and secondary voltage ratings are equal when it’s being used for isolation. The number of turns in the primary and secondary windings must be equal because there is only one power rating for the entire system. It’s a 1:1 ratio, which is the turns ratio (1:1).
The power rating of a transformer is equal to the greater of the product of the voltage and current in the primary circuit or the product of the voltage and current in the secondary circuit, with core losses disregarded.
The size of the load current connected to the secondary circuit of the transformer controls the sizes of the currents flowing in the primary and secondary circuits.
To avoid dangerously overheating the transformer, it is important to stay within the limits of the device’s power rating. Methodologically (with perfect efficiency assumed for all calculations):
VP × AP = VS × AS
Where
V ( ) = the voltage rating of the primary (P) and secondary (S) circuits
A ( ) = the full-load current rating of the primary (P) and secondary (S) circuits
The voltage ratio and the current ratio of a single transformer are inversely proportional to each other due to the transformer’s single power rating for both the primary and secondary circuits. By rearranging the preceding formula,
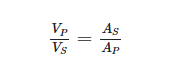
The primary current is increased to the larger secondary current value when a transformer is used to reduce the supply voltage. Multiples of 1 are used to represent the ratio of primary to secondary voltage. Primary current to secondary current is represented as a value between 1 and some multiple of 1.
The current ratio of a step-down transformer with a voltage ratio of 30:1 would be 1:100. (1:30).
This transformer has an inverse-proportional relationship between voltage and current, so the primary circuit’s current is always equal to the secondary current divided by 30.
Primary current is reduced to a smaller secondary current value when a transformer is used to increase the supply voltage. Primary-to-secondary voltage ratios are typically represented as integers between 1 and some multiple of 1. The primary current divided by the secondary current is represented by a number greater than 1.
The current ratio of a step-up transformer with a voltage ratio of 1:55 (1:55) is 55:1. (55:1).
For any given value of secondary current, this transformer’s primary current will always be equal to that value plus 55.
A transformer’s primary and secondary voltage ratings are equal when it’s being used for isolation. The primary and secondary currents must be equal because there is only one power rating for the entire system. The proportion between voltage and current is also 1:1. (1:1).
According to the technical definition, a single transformer’s primary can have either winding. Either winding is acceptable for the secondary. As the name implies, the primary winding is the one that is connected to the original power source (stepped down for a lower-circuit voltage, stepped up for a higher-circuit voltage, or merely electrically isolated for the same circuit voltage). To complete the circuit, the secondary winding of a transformer is wired to the device it is powering.
If the transformer isn’t being used at full capacity, its secondary load current may be significantly lower (for example, 200 amps available, but only a 60-amp load is connected to the transformer). Ohm’s law states that the secondary-circuit voltage rating and the resistance (or AC impedance) of the connected load determine the secondary-circuit current’s magnitude. The higher the secondary-circuit resistance, the lower the load current, and the reverse is also true. There is a one-to-one relationship between the secondary load current and the value of the primary circuit current (neglecting transformer losses).
No matter if the transformer is rated as a small signaling transformer (like a common doorbell supply), a small power transformer (as shown in the previous example), or a large power transformer, the ratios of voltage, current, and number of turns will remain the same (often found in unit substations).