Have you ever been stumped by a math problem that required you to use sin, cos, or tan? These three functions are commonly taught in trigonometry courses, but many people still struggle to understand how to use them properly. One common misconception is that sin, cos, and tan can only be used for right triangles. But is this really true?
It’s easy to see why so many people think that sin, cos, and tan are only for right triangles. The basic definition of these functions involves dividing one side of a right triangle by another. For example, sin is defined as the opposite side divided by the hypotenuse, while cos is the adjacent side divided by the hypotenuse. But does this mean that sin, cos, and tan can’t be used for other types of triangles?
The answer is no, sin, cos, and tan can be used for any triangle, whether it’s right or not. In fact, the key is to use the Law of Sines and Law of Cosines, which involve ratios of sides and angles in any triangle. So, the next time you encounter a math problem that involves sin, cos, or tan, don’t automatically assume that it’s only for right triangles. Keep an open mind and try to apply these functions to any type of triangle, and you might just surprise yourself with what you can solve.
Applications of Trigonometry in Real Life
Trigonometry is not just a mathematical concept, but it also has real-life applications that are relevant to everyday human lives. One of the most crucial applications of trigonometry is in the field of engineering and science. The concept of sin, cos, and tan is not just limited to right triangles, but it has various applications in real life.
Common Applications of Trigonometry:
- Architects use trigonometry to design buildings and calculate angles for aesthetic purposes and maximum sunlight exposure.
- Engineers use trigonometry to design bridges and buildings so that they can withstand external forces.
- Geologists use trigonometry to measure the height of mountains and other landforms accurately.
Trigonometry in Navigation and Astronomy
Another practical application of trigonometry is in Navigation and Astronomy. Sailors use trigonometry to calculate the position of a ship and plan voyages. Similarly, astronomers use trigonometry to calculate the distance between stars and planets.
Trigonometry also helps astronomers to understand the movement and growth of planets and stars. It is due to the application of Trigonometry that we know that the Earth rotates on its axis and revolves around the Sun.
Application of Trigonometric Ratios for Non-right Triangles
The sine, cosine, and tangent ratios can not only be used to calculate measurements in right-angled triangles but can also be used for obtuse or acute angles. To calculate the angle between two distant points, the cosine law can be used.
| Trig Ratios | Relationship between sides and angles of a right triangle |
|---|---|
| Sine ratio (sin) | $\sin A = \dfrac{Opposite}{Hypotenuse}$ |
| Cosine ratio (cos) | $\cos A = \dfrac{Adjacent}{Hypotenuse}$ |
| Tangent ratio (tan) | $\tan A = \dfrac{Opposite}{Adjacent}$ |
Trigonometry is a crucial aspect of mathematics with various practical applications in everyday life. Its applications range from engineering, architecture, navigation, astronomy, and more. By understanding the application of trigonometry, students can appreciate the importance of learning the concept and how it influences the world around them.
Pythagorean Theorem and Trigonometry
Understanding trigonometry starts with the Pythagorean Theorem and its applications in right triangles. The Pythagorean Theorem is a fundamental concept in mathematics that states that in a right triangle, the square of the hypotenuse (the longest side) is equal to the sum of the squares of the other two sides. Mathematically expressed:
a² + b² = c²
Where a and b are the lengths of the two shorter sides of the right triangle, and c is the length of the hypotenuse. This theorem is deeply intertwined with the concept of trigonometry, which deals with the relationships between the sides and angles of triangles.
- Sine: The sine of an angle in a right triangle is defined as the length of the opposite side divided by the length of the hypotenuse (SOH).
- Cosine: The cosine of an angle in a right triangle is defined as the length of the adjacent side divided by the length of the hypotenuse (CAH).
- Tangent: The tangent of an angle in a right triangle is defined as the length of the opposite side divided by the length of the adjacent side (TOA).
These formulas can be remembered using the mnemonic device SOH-CAH-TOA. While these formulas are strictly defined for right triangles, they have broader applications in calculus, physics, and engineering.
In addition, trigonometric functions are not limited to right triangles that have only integer values for their sides, as with Pythagorean triples such as 3-4-5 or 5-12-13. These functions can be applied to any triangle, including those with irrational sides or angles.
Applications of Trigonometry
Trigonometry has a wide range of applications in different fields, including:
- Architecture: Architects use trigonometry to calculate angles, heights, and distances in building designs.
- Navigation: Trigonometry is used in navigation to calculate the distance between two points, the heading or direction of travel, and the target location.
- Astronomy: Many astronomical calculations require the use of trigonometry to determine positions, distances, and areas of celestial objects.
Trigonometric Identities and Formulas
Trigonometric functions have several identities and formulas that can simplify calculations and make them more efficient. Some of the most essential trigonometric identities and formulas include:
| Function | Identity/Formula |
|---|---|
| Sine | sin(-x) = -sin(x) |
| Cosine | cos(-x) = cos(x) |
| Tangent | tan(-x) = -tan(x) |
| Pythagorean Identity | sin²(x) + cos²(x) = 1 |
| Sum and Difference Formulas | sin(x ± y) = sin(x)cos(y) ± cos(x)sin(y) |
| Double Angle Formulas | sin(2x) = 2sin(x)cos(x) |
By understanding and applying these identities and formulas, trigonometry can be used to solve a wide range of mathematical problems, from the simplest to the most complex.
Sine, Cosine and Tangent for Non-Right Triangles
While the sine, cosine, and tangent functions are typically associated with right triangles, they can also be used to solve non-right triangles. In fact, these functions are commonly used in trigonometry to solve problems involving any type of triangle.
However, when working with non-right triangles, the sine, cosine, and tangent functions are slightly different. Instead of simply using the ratios of the sides of a right triangle, we use something called the law of sines and the law of cosines to determine the angles and side lengths of a non-right triangle.
The Law of Sines and Cosines
- The law of sines is used to determine the side lengths and angles of any triangle. It states that the ratio of the length of a side of a triangle to the sine of the angle opposite that side is equal to the same ratio for all other sides and angles in the triangle.
- The law of cosines is used to determine the side lengths and angles of a non-right triangle when the lengths of two sides and the included angle are given. It can also be used to find the length of a side when all three angles of a triangle are known.
Different Ways of Using Sine, Cosine and Tangent for Non-Right Triangles
One way to use the sine, cosine, and tangent functions for non-right triangles is to use the law of sines and the law of cosines to determine the unknown sides and angles of the triangle. Another way is to use something called the area formula, which involves the sine function. This formula states that the area of a triangle is equal to one-half the product of two sides and the sine of the included angle.
For example, if we know two sides and the included angle of a triangle, we could use the area formula to find the area of the triangle. We could also use the law of cosines to find the length of the third side and then use the law of sines to find the remaining angles.
Conclusion
While sine, cosine, and tangent are commonly associated with right triangles, they are also useful for solving problems involving non-right triangles. By using the law of sines, the law of cosines, and the area formula, we can determine the angles and side lengths of these more complex triangles. With practice and understanding of the underlying principles, anyone can use these tools to solve trigonometric problems involving non-right triangles.
| Function | Definition |
|---|---|
| Sine | The sine of an angle is the ratio of the length of the side opposite the angle to the length of the hypotenuse in a right triangle. |
| Cosine | The cosine of an angle is the ratio of the length of the adjacent side to the length of the hypotenuse in a right triangle. |
| Tangent | The tangent of an angle is the ratio of the length of the side opposite the angle to the length of the adjacent side in a right triangle. |
Trigonometry and Unit Circles
Trigonometry is the branch of mathematics that deals with the study of triangles and the relationship between their sides and angles. It involves three main functions: sine, cosine, and tangent. These functions are commonly abbreviated as sin, cos, and tan, respectively. The fundamental concept behind trigonometry is the unit circle, which is a circle with a radius of one unit.
- The sine function (sin) is defined as the ratio of the side opposite to an acute angle in a right-angled triangle to the hypotenuse.
- The cosine function (cos) is defined as the ratio of the adjacent side to an acute angle in a right-angled triangle to the hypotenuse.
- The tangent function (tan) is defined as the ratio of the side opposite to an acute angle in a right-angled triangle to the adjacent side.
It is a common misconception that sin, cos, and tan can only be used with right triangles. However, these functions can also be used with unit circles to find the values of angles in any type of triangle, including acute, obtuse, or right triangles.
When we plot the angle in the unit circle, the x-coordinate of the point where the angle intersects the unit circle is equal to the cosine of the angle, and the y-coordinate is equal to the sine of the angle. For instance, an angle of 30 degrees would intersect the unit circle at the point with (x, y) coordinates of (0.87, 0.5).
The following table shows the trigonometric values of commonly used angles:
| Angle (degrees) | Sine (sin) | Cosine (cos) | Tangent (tan) |
|---|---|---|---|
| 0° | 0 | 1 | 0 |
| 30° | 0.5 | 0.87 | 0.58 |
| 45° | 0.71 | 0.71 | 1 |
| 60° | 0.87 | 0.5 | 1.73 |
| 90° | 1 | 0 | undefined |
Trigonometry is a crucial concept in fields such as engineering, physics, and mathematics, and its practical applications can be seen in areas such as navigation, astronomy, and surveying. Understanding how to use sin, cos, and tan can lead to a better understanding of the properties and relationships of triangles, as well as a deeper appreciation for the fundamental principles of mathematics.
Inverse Trigonometric Functions
Trigonometry is a branch of mathematics that deals with the relationships between the sides and angles of triangles. The three main trigonometric functions are sine (sin), cosine (cos), and tangent (tan). These functions are used to solve for missing sides and angles in right triangles. However, what happens when we need to solve for angles in non-right triangles? This is where inverse trigonometric functions come in.
- The inverse sine function, denoted as sin-1, gives us the angle whose sine is a given value.
- The inverse cosine function, denoted as cos-1, gives us the angle whose cosine is a given value.
- The inverse tangent function, denoted as tan-1, gives us the angle whose tangent is a given value.
The inverse trigonometric functions are also known as arc functions or anti-trigonometric functions. They are used to solve for angles in non-right triangles, as well as in various fields such as engineering, physics, and navigation.
It’s important to note that the domain of the inverse trigonometric functions is limited. For example, the domain of sin-1(x) is -1 ≤ x ≤ 1. If x is outside this range, the function is undefined. This is because the sine function only takes on values between -1 and 1, and we cannot take the inverse sine of a value outside this range.
When using inverse trigonometric functions, it’s also important to be aware of the various identities and formulas that can simplify calculations. For example, the Pythagorean identity, sin2(θ) + cos2(θ) = 1, can be used to solve for missing angles or sides in non-right triangles.
| Trigonometric Function | Inverse Trigonometric Function |
|---|---|
| sin(θ) | sin-1(x) |
| cos(θ) | cos-1(x) |
| tan(θ) | tan-1(x) |
Overall, inverse trigonometric functions allow us to solve for angles in non-right triangles, expanding the range of applications for trigonometry beyond just right triangles.
Trigonometric Identities and Equations
Trigonometric functions such as sine, cosine, and tangent are often used to represent the relationship between the sides and angles of a right triangle. However, contrary to popular belief, they are not limited to right triangles alone. In fact, they have many other important roles in the world of mathematics, including applications in calculus, physics, and engineering.
Trigonometric identities and equations are essential tools in working with trigonometric functions. These identities are mathematical equations that are true for all values of the variables in the equation. They allow mathematicians and scientists to simplify expressions and solve complex problems involving trigonometric functions.
One of the most well-known trigonometric identities is the Pythagorean theorem, which states that in a right triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides. This can be expressed algebraically using the trigonometric functions as:
| Pythagorean theorem: | sin2(θ) + cos2(θ) = 1 |
|---|
Another important group of trigonometric identities are the reciprocal identities. These identities show the relationship between the six trigonometric functions: sine, cosine, tangent, cosecant, secant, and cotangent. The reciprocal identities are:
- csc(θ) = 1/sin(θ)
- sec(θ) = 1/cos(θ)
- cot(θ) = 1/tan(θ) = cos(θ)/sin(θ)
Beyond the basic identities, there are many other trigonometric identities and equations that are used in various applications. Whether you are a student studying calculus, a physicist solving complex equations, or an engineer designing a new structure, understanding trigonometric identities and equations is essential to success in these fields.
Trigonometric Functions and Graphing
Trigonometric functions, namely sine (sin), cosine (cos), and tangent (tan), are often associated with right triangles. These functions help us solve problems that involve sides and angles in triangles. However, sin, cos, and tan are not exclusive to right triangles.
The functions are defined using the ratios of the sides in a right triangle. For a given angle in a right triangle, sin is the ratio of the opposite side to the hypotenuse, cos is the ratio of the adjacent side to the hypotenuse, and tan is the ratio of the opposite side to the adjacent side.
- Sin = opposite / hypotenuse
- Cos = adjacent / hypotenuse
- Tan = opposite / adjacent
These ratios are useful not just in geometry, but in other fields such as physics and engineering. They can be used to analyze waves, vibrations, and oscillations.
When graphing these functions, they result in a wave-like pattern, known as a periodic function. The amplitude of the wave equals the maximum value of the function, while the period is the length of the wave cycle. The period is defined as 2π for sin and cos functions and π for the tan function. The x-axis represents the angle, while the y-axis represents the value of the function. The graphs of these functions are continuous and repeat after every period.
| Function | Graph |
|---|---|
| Sin(x) | 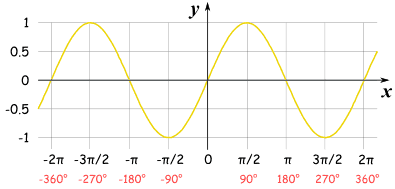 |
| Cos(x) | 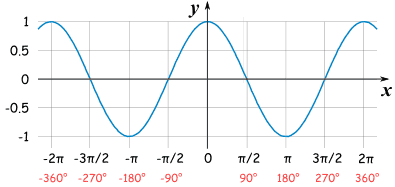 |
| Tan(x) | 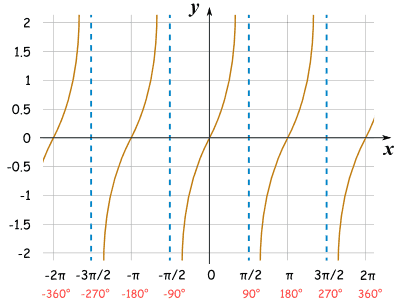 |
By understanding the properties of sin, cos, and tan functions, we can solve problems involving angles and sides in a triangle, as well as in other applications in science and engineering. Graphing these functions allows us to visualize their behaviors and patterns and serves as a valuable tool in analyzing data and phenomena.
FAQs about Is Sin Cos Tan Only for Right Triangles
1. What are sin cos tan used for in trigonometry?
Sin, cos, and tan are used to find the ratios of the sides in a right triangle.
2. Are sin cos tan only used in right triangles?
Yes, sin cos tan are only used for finding angles and sides in right triangles.
3. Why can’t sin cos tan be used for non-right triangles?
Because the ratios of the sides in non-right triangles are not constant and vary depending on the angles.
4. Can’t sin cos tan be generalized for all triangles?
No, sin cos tan are specific to right triangles only and cannot be generalized for all triangles.
5. Can sin cos tan be used to find angles in a right triangle?
Yes, sin cos tan can be used to find angles in a right triangle by using inverse functions like arcsin, arccos, and arctan.
6. Do we need to know sin cos tan to solve trigonometry problems?
Yes, sin cos tan are fundamental concepts in trigonometry and are necessary to solve many problems in the subject.
7. Is it important to know when to use sin cos tan in a problem?
Yes, knowing when to use sin cos tan can help simplify trigonometry problems and avoid making errors.
Closing thoughts
Now that you know more about sin cos tan and their applications in trigonometry, you can approach right triangle problems with more confidence. Remember to use these functions only for right triangles and to always double-check your answers. Thanks for reading and don’t forget to come back for more helpful articles in the future!
