Some common phrases for describing alternating waveforms are as follows:
- A ‘periodic function’ is a cyclical, ever-repeating waveform.
- The frequency of a wave is defined as the number of times that wave is repeated in one second, measured in cycles per second or hertz.
- In physics, the ‘period’ is the amount of time it takes for one cycle to repeat itself; it is defined as 1 minus the reciprocal of the frequency (or 1/f seconds).
- A voltage or current waveform’s instantaneous value is its value at a single point in time.
- Sine waves are typically described using different values, and calculations on sinusoidal values are typically done using different values.
Average Value of Sine Wave
Since the magnitude of an alternating sine wave varies continuously, a meaningful standard must be applied when describing its value as a voltage or a current. To calculate the mean value of a sinusoidal function, divide the period by 2/π or 0.637.
Therefore, you can determine the typical voltage or current by:
Vav = 0.637 × Vmax
Iav = 0.637 × Imax
Please take into account that these expressions are valid only for sine waves.
Since the direction of flow reverses halfway through the cycle, the average value of the second half-cycle is 0.637, and the average flow for a complete cycle is zero. Normal ac circuits don’t make as much use of average values as do those that involve DC conversion.
To compare the efficiency or power of alternating and direct currents on the basis of average values would be inappropriate. Therefore, it is critical to have a second metric by which the actual effects of alternating waves can be compared.
Root–Mean–Square Value of Sine Wave
The root-mean-square (RMS) value of a sine wave is calculated in order to determine its ability to produce the same heating effect as DC. The term alludes to the calculative process involved in arriving at the answer. Thankfully, there is another way to justify the validity of calculus.
Experimentally or mathematically, it is shown that the power produced by using maximum values of voltage and current is exactly half of the power produced by using the same DC values. And I mean that literally
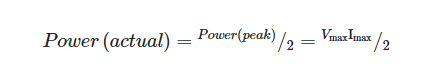
Since the maximum values of both the voltage and the current must be adjusted by the RMS factor (since the current is proportional to the applied voltage). And I mean that literally
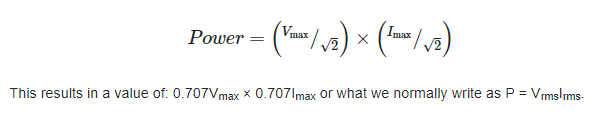
In order to achieve the same results as a DC voltage, the RMS value is often referred to as the “effective voltage” that will generate a “effective current flow”
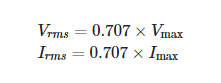
Please take into account that these expressions are valid only for sine waves.
Any ac value is to be taken as the RMS value unless otherwise specified. The standard voltage for a home’s electrical system is referred to as 230 V, but 325 V is the maximum allowed.
Take note that the RMS value of ac is what is meant throughout this book unless otherwise specified.
The expression yields the maximum output of a 230 V RMS supply:
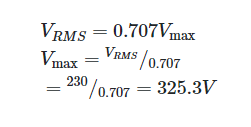
Crest Factor for Sine Wave
The crest factor, also known as the maximum-to-root-mean-square ratio, is a common metric for describing the topology of waveforms.
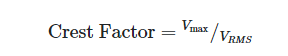
For a sine wave, for instance:
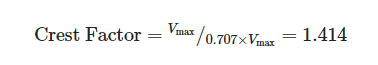
In its ratio form, the crest factor has no inherent units.
For ac waveforms of a given RMS value, the crest factor is helpful in indicating the maximum EMF that can be expected, and thus the value of the voltage that the insulation must withstand.
Form Factor for Sine Wave
Form factor is defined as the following ratio for any given waveform:
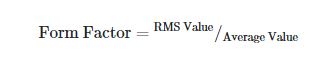
Seeing the overall form of an ac waveform can be helpful. For a sine wave, for instance:
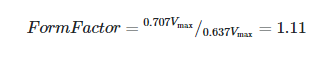
The form factor is greater than 1.11, indicating a peakier waveform compared to a pure sine wave. When the form factor is less than 1.11, however, the wave looks more like a triangle than a sine. To give just one example, a square wave has a form factor of 1.
Peak-To-Peak Value for Sine Wave
In some cases, the difference between a wave’s positive and negative peaks will be significant. This is equivalent to twice the maximum value in either direction for most alternating waveforms. If you have a 230 V ac supply, for instance, you can calculate the maximum voltage by subtracting 230 from 0.7075.
Multiplying 230 by 1.414 (the reciprocal of 0.707 is 1.414, which is equal to √2) yields the same result. The maximum voltage obtained using either technique is 325.3 V. If we double this number, we get 650.6 V for the peak-to-peak value. Since there is no zero voltage line on the trace of a cathode ray oscilloscope, this is of great help when determining the magnitude of alternating waveforms.
